A new Control Flow Graph based heuristic for Diaphora

Some weeks ago I decided to code a new heuristic based on one of the great ideas that Huku, a researcher from Census Labs I met in some private event, proposes in his paper Efficient Features for Function Matching between Binary Executables.

All features are equal, but some features are more equal than others

In Huku’s paper, he proposes to extract features from the Control Flow Graphs (CFGs) considering that each basic block (each node) can be special and classifies basic blocks in 7 categories: normal, entry points, exit points, traps, self-loops, loop heads and loop tails. In the same way, he classifies 4 different kinds of edges: basis, forward, back edges and cross-links. There are various other good looking ideas in that paper like, for example, the instructions histograms, which classifies instructions in 4 categories based on their functionality (arithmetic, logic, data transfer, redirection), but I haven’t implemented anything based on the other ideas, for now.

The КОКА algorithm

In the case of the algorithm I have developed (КОКА, from Koret-Karamitas) and based on the idea of “different basic blocks and edges are different interesting pieces of information”, I have created a new heuristic for Diaphora that gets features at function, basic block, edge and instruction level, assigns a different prime value to each different feature and then generates a hash by just mutiplying all the values (a small-primes-product, SPP). My algorithm extracts the following features:

• For each basic block in each function, multiply a prime value assigned to each different type of basic block (in the Huku’s case he considers 7 categories, in my case I only consider 3 categories: entry/exit points and “normal” nodes).
• For each edge in each function, multiply a prime value assigned to each different type of edge. In my case I only consider, for now, 2 different types of edges; Huku considers 4.
• For each instruction, multiply a prime value assigned to each instruction that is considered. In my case I only consider a reduced number of types of instructions: in-calls, out-calls and data references.
• At function level, again, multiply a prime value assigned to each feature I consider. In my case I consider the number of loops, the number of strongly connected components, if the function returns or not, if it’s a library function and if it’s a thunk function or not.

After all these four steps, the final generated ‘hash’ is a large number result of the multiplication of the various prime numbers assigned to features of the function. If you’re curious about why I decided not to add the various different basic block and edge types that Huku mentions in his paper, it is because, during my (very basic) testing I noticed that some features (like loop heads/tails) were causing some mismatches for functions that are the same when comparing binaries compiled for different architectures. Also, because I didn’t want to copy the algorithm but, rather, based on his ideas create my own one.

Results of the fuzzy graph hash

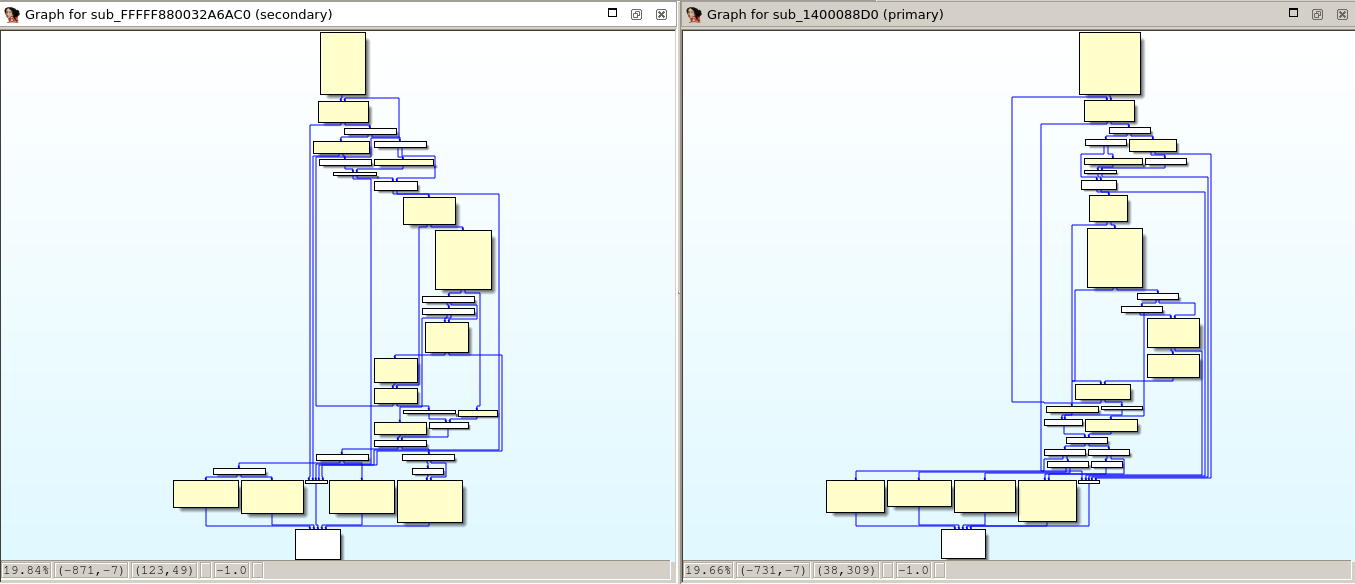
The algorithm was made with the idea of making it somehow ‘fuzzy’ but not too fuzzy or, otherwise, it would cause too many false positives. Let’s run the script calculating the hash against the ‘ls’ binary from Ubuntu 16.04 x86_64 (with SHA1 hash b79f70b18538de0199e6829e06b547e079df8842). IDA 7.2 discovered 416 functions during its initial analysis. Running the script against that binary it will print out the hash for each function in the database and, at the end, show the different unique hashes it discovered. In this example, it says it discovered 141 unique hashes. It means that for this database, the hash identifies unequivocally 141 functions out of 416, that’s the 33.89% of the functions for just one single heuristic. Let’s see now some multi-matches; that’s it, hashes that match multiple functions… For example, given the hash 39278199524711331437958782332054597998538807300237778665425000000 it matches the functions at addresses 0x00407b40 and 0x00407cd0. If we take a look to their control flow graphs we will see that they are identical:

As we can see, it’s pretty much the same function. The only difference is that one calls strcmp() and the other calls a wrapper for strcoll(). The hash I chosen is somehow ‘big’, let’s try now with a smaller hash like for example 8031387939300; it will match the functions at 0x00405120, 0x00405170, 0x0040f190, 0x0040f3c0 and 0x00413b9c. If we take a look to them we will see small functions like the following ones:

.text:0000000000413B9C sub_413B9C      proc near
.text:0000000000413B9C ; __unwind {
.text:0000000000413B9C                 mov     edx, offset unk_61F360
.text:0000000000413BA1                 mov     esi, offset _localtime_r
.text:0000000000413BA6                 jmp     sub_413723
.text:0000000000413BA6 ; } // starts at 413B9C
.text:0000000000413BA6 sub_413B9C      endp

.text:0000000000405120 sub_405120      proc near
.text:0000000000405120 ; __unwind {
.text:0000000000405120                 mov     rsi, [rsi]
.text:0000000000405123                 mov     rdi, [rdi]
.text:0000000000405126                 jmp     _strcmp
.text:0000000000405126 ; } // starts at 405120
.text:0000000000405126 sub_405120      endp

.text:000000000040F3C0 sub_40F3C0      proc near
.text:000000000040F3C0 ; __unwind {
.text:000000000040F3C0                 mov     ecx, offset unk_61E5A0
.text:000000000040F3C5                 mov     rdx, 0FFFFFFFFFFFFFFFFh
.text:000000000040F3CC                 jmp     sub_40EAA0
.text:000000000040F3CC ; } // starts at 40F3C0
.text:000000000040F3CC sub_40F3C0      endp

As we can see, all the functions are pretty similar. There are differences in what they do, of course, but at the number of cross references, data references, basic blocks, edges, calls, etc… they are equal and it is this algorithm’s sole purpose.

The new heuristic

As previously mentioned, I’ve added a new heuristic to Diaphora based on the output of this algorithm. As with MD-Indices, only hashes that are ‘rare enough’ are considered. It turns out that the reliability of the matches discovered by this hash is very high and, as so, the results of the heuristic ‘Same rare КОКА Hash’ are always assigned to either the “Best” or “Partial” tabs but, in case of partial matches, with a high similarity ratio, usually something higher than 0.98 which is very-very high. But, most of the time, as shown in the picture bellow, such matches are always ‘perfect’ ones:

The independent library

While this heuristic has been created with the idea of using it in Diaphora, it can be used half-independently. You just need to put in the same folder the scripts graph_hashes.py and tarjan_sort.py from Diaphora or, alternatively, copy the directories jkutils and others to some directory where your script will reside, and in any of these 2 ways you can use independently this algorithm for your own tasks by writing an IDA Python script similar to the following one:

from idaapi import *

# Remove the "jkutils." part if you just copied graph_hashes.py & tarjan_sort.py 
from jkutils.graph_hashes import CKoretKaramitasHash

for f in Functions():
  hasher = CKoretKaramitasHash()
  final_hash = hasher.calculate(f)
  print("0x%08x: %s" % (f, str(final_hash)))

Porting the algorithm and final remarks.

The code for this CFGs hashing algorithm has been pushed to the Diaphora’s GitHub repository and is now available here.

The algorithm is rather easy to port to other reverse engineering frameworks like Binary Ninja or Radare2 but, for now, it’s left as an exercise for the reader. It would be very cool to have it working in Radare2 to, for example, cluster and index malware with only open source tools. Perhaps it could be a great new feature for Cosa Nostra and MalTindex.

And… that’s all! I hope you like both this blog post and the new heuristic, and don’t forget to check Huku’s paper!